AlexCTF 2017 write ups
Introduction
I took part in the AlexCTF this weekend, which was an online jeopardy-style CTF. Thanks to the Greunion team for having me!
CR2: Many time secrets (100 points)
This challenge is a classical OTP cryptographic challenge. We have several messages all XORed with the same key, which is the flag.
However, since we know that the flag has to follow a specific format
(ALEXCTF{[A-Za-z0-9_]*}), we have the beginning of the key, which allows to
decrypt the beginning of each message!
Dear Fri
nderstoo
sed One
n scheme
is the o
hod that
proven
ever if
cure, Le
gree wit
ncryptio
We can easily guess the next character for some of the messages, which in turn gives us the next character of the key. All what is left to do is repeating the process until the end of the key!
The following Python script has been used to make the process easy:
def xor(a, b):
return ''.join(chr(ord(x) ^ ord(y)) for x, y in zip(a, b))
def help_find_key(msgs):
key = 'ALEXCTF{'
max_len = max(map(len, msgs))
while True:
print '\n>>', key.encode('string-escape')
for i, msg in enumerate(msgs):
print '%-2d' % i, xor(key, msg)
if len(key) == max_len:
break
i = int(raw_input('\nline: '))
c = raw_input('char: ')
key += xor(msgs[i][len(key)], c)
with open('msg') as f:
help_find_key([x.strip().decode('hex') for x in f])
After a few iterations, the flag is ours!
>> ALEXCTF{HERE_GOES_THE_KEY}
0 Dear Friend, This time I u
1 nderstood my mistake and u
2 sed One time pad encryptio
3 n scheme, I heard that it
4 is the only encryption met
5 hod that is mathematically
6 proven to be not cracked
7 ever if the key is kept se
8 cure, Let Me know if you a
9 gree with me to use this e
10 ncryption scheme always.
CR4: Poor RSA (200 points)
We have an RSA public key, and what is likely to be the flag encrypted with the corresponding private key.
$ openssl rsa -pubin -in key.pub -text -noout
Public-Key: (399 bit)
Modulus:
52:a9:9e:24:9e:e7:cf:3c:0c:bf:96:3a:00:96:61:
77:2b:c9:cd:f6:e1:e3:fb:fc:6e:44:a0:7a:5e:0f:
89:44:57:a9:f8:1c:3a:e1:32:ac:56:83:d3:5b:28:
ba:5c:32:42:43
Exponent: 65537 (0x10001)
With a key length smaller than 512 bits, it should not be too difficult to factor. Indeed, a lookup on the factordb.com website reveals the two factors.
All what is left is converting all parameters in a format openssl
understands, and decrypt the flag:
import gmpy2
p = 863653476616376575308866344984576466644942572246900013156919
q = 965445304326998194798282228842484732438457170595999523426901
e = 65537
d = gmpy2.invert(e, (p - 1) * (q - 1))
print '''asn1=SEQUENCE:rsa_key
[rsa_key]
version=INTEGER:0
modulus=INTEGER:{n}
pubExp=INTEGER:{e}
privExp=INTEGER:{e1}
p=INTEGER:{p}
q=INTEGER:{q}
e1=INTEGER:{e1}
e2=INTEGER:{e2}
coeff=INTEGER:{coeff}'''.format(
n=p * q,
e=e,
p=p,
q=q,
e1=d % (p - 1),
e2=d % (q - 1),
coeff=gmpy2.invert(q, p),
)
A few openssl commands later, we have the flag!
$ ./build.py > priv.conf
$ openssl asn1parse -genconf priv.conf -out priv.der -noout
$ base64 -d flag.b64 | openssl rsautl -decrypt -inkey priv.der -keyform der
ALEXCTF{SMALL_PRIMES_ARE_BAD}
CR5: Bring weakness (300 points)
We got this PRNG as the most secure random number generator for cryptography
Can you prove otherwise
nc 195.154.53.62 7412
After connecting on the server, the challenge is clear: we can generate as many random numbers in a raw as we want, and then we need to predict the next 10 numbers.
$ ncat 195.154.53.62 7412
Guessed 0/10
1: Guess the next number
2: Give me the next number
2
401969523
Guessed 0/10
1: Guess the next number
2: Give me the next number
2
1144833507
Guessed 0/10
1: Guess the next number
2: Give me the next number
1
Next number (in decimal) is
The usual issue with PRNG is due to their design: they are usually based on an internal state. Each time output is generated, the internal state is changed. Depending on the size of the internal state, the PRNG output will cycle sooner or later.
In our case, it seems that the generated numbers are 32 bits long. But that does not prove anything about the internal state, so let's ask for quite a lot of output, and analyse it:
$ yes 2 | ncat 195.154.53.62 7412 | grep -v ' ' | head -n 100000 > out
$ wc -l out
100000 out
$ sort -u out | wc -l
32768
As we can see, we have only 2^15 different outputs out of the 100000 samples
we asked. A closer look reveals that the generated numbers are indeed generated
in a loop, with a full cycle of
2^15.
So our attack is simple:
- Ask for 32768 consecutive outputs
- Predict the next outputs now that we have the full cycle
This is what the following Python script does:
from socket import socket
class Run(object):
def __init__(self):
self.cycle = {}
self.s = socket()
self.s.connect(('195.154.53.62', 7412))
self.buf = ''
def Run(self):
print '[*] Get full cycle'
self.get_full_cycle()
print '[*] Predict numbers'
n = self.get_nb()
for _ in range(11):
n = self.cycle[n]
self.s.sendall('1\n%d\n' % n)
print '[*] Print flag'
print self.recv(lambda x: 'ALEXCTF' in x)
def recv(self, test):
while True:
if '\n' not in self.buf:
self.buf += self.s.recv(1024)
continue
val, self.buf = self.buf.split('\n', 1)
if test(val):
return val
def get_nb(self, send=True):
if send:
self.s.sendall('2\n')
return int(self.recv(lambda x: all(c in '0123456789' for c in x)))
def get_full_cycle(self):
self.s.sendall('2\n' * 0x8001) # sending all at once for speedup
p = self.get_nb(False)
for _ in range(0x8000):
n = self.get_nb(False)
self.cycle[p] = n
p = n
if __name__ == '__main__':
Run().run()
Running it reveals the flag as expected, and getting the full cycle took less than 3 seconds, which was a good surprise.
$ ./run.py
[*] Get full cycle
[*] Predict numbers
[*] Print flag
flag is ALEXCTF{f0cfad89693ec6787a75fa4e53d8bdb5}
Fore2: Mail client (100 points)
$ file core.1719
core.1719: ELF 64-bit LSB core file x86-64, version 1 (SYSV), SVR4-style, from 'mutt', real uid: 0, effective uid: 0, real gid: 0, effective gid: 0, execfn: '/usr/bin/mutt', platform: 'x86_64'
In this challenge, we have a mutt coredump, and we need to extract the email
and password of the user account and send them to a remote service.
We look at the strings of the coredump, and quickly find a password:
$ strings core.1719 | grep pass | head -3
passwd
tp_pass = "e. en kv,dvlejhgouehg;oueh fenjhqeouhfouehejbge ef"
unset imap_passive
This seems to be from the configuration file of mutt, but the string tp_pass
is probably for SMTP (two first bytes missing), not IMAP.
Let's see if that password is stored somewhere else in the core dump:
$ strings core.1719 | fgrep 'fenjhqeouhfouehejbge' -C1
dksgkpdjg;kdj;gkje;gj;dkgv a enpginewognvln owkge noejne
e. en kv,dvlejhgouehg;oueh fenjhqeouhfouehejbge ef
gpg --no-verbose --export --armor %r
--
172.17.0.2 78932fb3f2a0
tp_pass = "e. en kv,dvlejhgouehg;oueh fenjhqeouhfouehejbge ef"
set from = "alexctf@example.com"
So we have the email address, and also an other line just before the SMTP password… maybe it is the IMAP password?
$ ncat 195.154.53.62 2222
Email: alexctf@example.com
Password: dksgkpdjg;kdj;gkje;gj;dkgv a enpginewognvln owkge noejne
1 new unread flag
ALEXCTF{Mu77_Th3_CoRe}
We were lucky this time!
RE2: C++ is awesome (100 points)
This is a classical crackme: the re2 binary is taking a flag as the first
parameter, and tels us if the flag is valid or not.
I remember reading an article from Jonathan Salwan, where he uses Intel PIN to bruteforce a flag one character at a time.
Indeed, if the program checks the flag character by character, we can try all possible values for the first character. The good one will be the one for which the more CPU instructions have been run.
I edited his Python code to the following:
import commands
charset = 'abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ0123456789_'
def count(flag):
cmd = "./pin -t source/tools/ManualExamples/obj-intel64/inscount0.so" \
" -- ./re2 ALEXCTF{%s} > /dev/null; cat inscount.out" % flag
res = int(commands.getstatusoutput(cmd)[1].split("Count")[1])
print res, flag
return res
flag = ''
while True:
best_t = last_t = count(flag)
best_c = ''
for c in charset:
t = count(flag + c)
if t > best_t:
best_t = t
best_c = c
print
if best_t == last_t:
print 'FOUND: ALEXCTF{%s}' % flag
break
flag += best_c
And run it: it just worked under 10 minutes!
$ time ./run.py
2053431
2053431 a
2053431 b
--<snip>--
FOUND: ALEXCTF{W3_L0v3_C_W1th_CL45535}
real 9m59.075s
user 8m18.984s
sys 1m28.124s
RE4: unVM me (250 points)
This challenge starts with a compiled Python code.
$ file unvm_me.pyc
unvm_me.pyc: python 2.7 byte-compiled
We use the corresponding uncompyle version and retrieve the following Python code.
import md5
md5s = [174282896860968005525213562254350376167L,
137092044126081477479435678296496849608L,
126300127609096051658061491018211963916L,
314989972419727999226545215739316729360L,
256525866025901597224592941642385934114L,
115141138810151571209618282728408211053L,
8705973470942652577929336993839061582L,
256697681645515528548061291580728800189L,
39818552652170274340851144295913091599L,
65313561977812018046200997898904313350L,
230909080238053318105407334248228870753L,
196125799557195268866757688147870815374L,
74874145132345503095307276614727915885L]
print 'Can you turn me back to python ? ...'
flag = raw_input('well as you wish.. what is the flag: ')
if len(flag) > 69:
print 'nice try'
exit()
if len(flag) % 5 != 0:
print 'nice try'
exit()
for i in range(0, len(flag), 5):
s = flag[i:i + 5]
if int('0x' + md5.new(s).hexdigest(), 16) != md5s[i / 5]:
print 'nice try'
exit()
print 'Congratz now you have the flag'
So the flag is cut in 13 parts of 5 characters, and we have the md5 hash of each part. Of course, we like the md5 hashes better in hex format, so let's convert them with some Python:
for m in md5s:
print '%032x' % m
Then, we could use John the Ripper, but since the plaintexts are only 5 characters long, rainbow tables are the way to go!
Or, if we are lazy, just ask an online service like hashkiller:
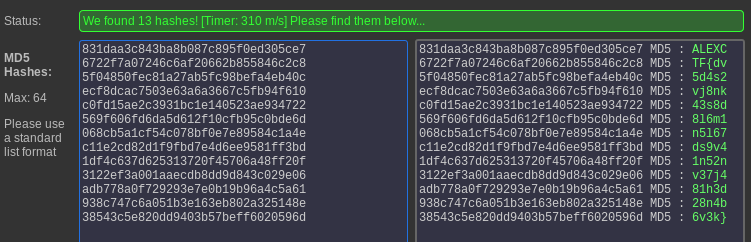
This gives us the flag:
ALEXCTF{dv5d4s2vj8nk43s8d8l6m1n5l67ds9v41n52nv37j481h3d28n4b6v3k}.
Conclusion
This is the end of the AlexCTF challenge, which was long enough! 48 hours CTFs are quite a time investment. Nothing is like trying to extract a flag from a lolcat at 10:30pm (that was our last flag to score)…
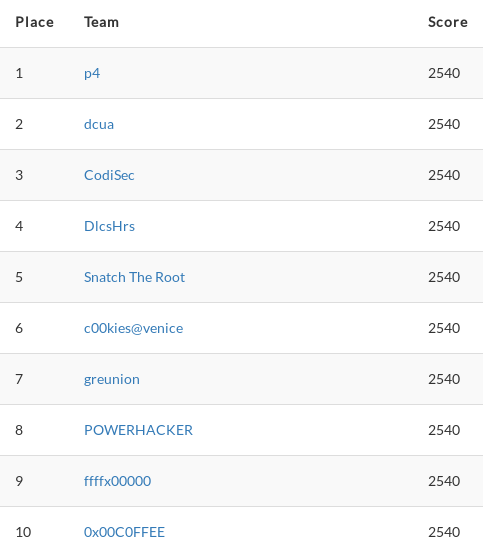
At the end, we solved every single challenge and ranked 7 out of 1000+ participants!