CSAW CTF 2018 write ups

Sep 17 2018

Introduction

Once more, I've been called by my team, Greunion for a CTF during a week-end. This time, it was CSAW CTF!

Bellow are short write-ups for two crypto challenges.

Flatcrypt (crypto 100)

TL;DR: Oracle on the length of the plaintext after zlib compression.

We are provided with the source code of a Python server. The provided plaintext is appended to the flag, compressed with zlib, and finally encrypted with AES.

AES is used in CTR mode. The key is static, but the nonce is properly random, so nothing to be exploited there. However, in CTR mode, the ciphertext has the same length as the plaintext.

In other words, we have an oracle telling the length of the plaintext after zlib compression. This looks closely to the crypto 250 challenge from Plaid CTF 2013.

In short, the output of zlib will have a smaller length if there are more repetitions in the input. For example, if the flag is flag, let's concatenate the following and see the output length:

aaaaa gives an output of 14 chars (there are 5 a at the end);
ggggg gives an output of 13 chars (there are 6 g at the end).

We can deduce that the last letter of the flag is g.

I wrote the following code to find the flag:

from pwn import *
from functools import partial
import string

def get_len(r, data):
    r.recvuntil('\n')
    r.sendline(data)
    line = r.recvuntil('\n')[2:-3].decode('string-escape')
    return len(line)


def solve(oracle, suffix, charset):
    out = []
    for c in charset:
        data = c + suffix
        data *= 5
        while len(data) < 20:
            data += '<'  # pad
        out.append((c, oracle(data)))
    max_value = max(out, key=lambda o: o[1])[1]
    return [o[0] for o in out if o[1] != max_value]


def solve_all(oracle):
    suffixes = ['']
    charset = string.ascii_lowercase + '_'
    while suffixes:
        new_suffixes = []
        for suffix in suffixes:
            if suffix:
                # skip loops at the right of suffix
                if suffix.endswith(suffix[-1:] * 3):
                    continue
                if suffix.endswith(suffix[-2:] * 3):
                    continue
            chars = solve(oracle, suffix, charset)
            if not(chars):
                yield suffix
                continue
            for char in chars:
                new_suffixes.append(char + suffix)
        log.info(suffixes)
        suffixes = new_suffixes

with remote('crypto.chal.csaw.io', 8042) as r:
    for solved in solve_all(partial(get_len, r)):
        log.success(solved)

This outputs the following candidates:

gogoo
rime_doesnt_have_a_logo
rime_doesnt_have_a_logoo
rime_doesnt_have_a_logogo

The first character is missing, but we can guess that the flag is indeed crime_doesnt_have_a_logo as a reference to the CRIME attack.

Collusion (crypto 500)

TL;DR: In an RSA-like cryptosystem, obtain a multiple of phi to factor n.

We are provided some go code implementing an RSA-like cryptosystem, together with the output of it encrypting the flag. We will use the usual RSA notations:

n = p * q  (with p and q both primes)
phi = (p - 1) * (q - 1)

We also have the following from reading the code:

p = 2 * p' + 1  (with p' prime)
q = 2 * q' + 1  (with q' prime)
X = random()
r = random()

The code is basically doing the following:

Na = DecrypterId('Alice')
Nb = DecrypterId('Bob')
Nc = DecrypterId('Carol')

Da = inverse(Na, phi)
Db = inverse(Nb, phi)
Dc = inverse(Nc, phi)

V = 3 ** ((Na + X) * r)
K = 3 ** r
shared = sha256(K)
Nonce, Body = AES-GCM(shared).encrypt(flag)

However, we only are provided with n, Db, Dc, V, Nonce, Body.

First, we notice that if we recover Da, we could compute V ** Da modulo n, which equals K. At that point we have everything to decode body and recover the flag.

Now, we can recover Na, Nb and Nc since they are computed in a deterministic way from the strings Alice, Bob and Carol. The following code was used:

package main

import (
    "math/big"
    "fmt"
    "log"
)

func main() {
    log.SetFlags(log.LstdFlags | log.Lshortfile)

    n := new(big.Int)
    n, ok := N.SetString("6208...snip...2513", 10)
    if !ok {
        log.Fatal(ok)
    }

    na, err := DecrypterId("Alice", n)
    if err != nil {
        log.Fatal(err)
    }
    fmt.Printf("Alice -> %s\n", na.String())

    // same for Bob and Carol
}

Now, we have the following equations:

(1): Db * (Nb + X) = 1 mod phi
(2): Dc * (Nc + X) = 1 mod phi

There are still too many unknown variables to solve, but we can remove X by combining (1) and (2):

Dc * (1) - Db * (2) gives:
s = Dc * Db * (Nc - Nb) + Dc - Db = 0 mod phi

In other words, we have s which is a multiple of phi. Turns out having a multiple of phi is enough to factor n:

The second link gives us the code to recover one factor of n. All is left is to compute the missing variables from there and we recover the flag.

from hashlib import sha256
from Crypto.Cipher import AES
from Crypto.Util.number import long_to_bytes, inverse
from sci_crypt_post import split_using_lambda

n = 6208...snip...2513
Db = 5334...snip...0601
Dc = 4650...snip...9571
V = 5842...snip...1631
Nonce = "2NXgQhueKbVm5Pd8".decode('base64')
Body = "0ZWA...snip...zA==".decode('base64')
Na = 5686...snip...1581
Nb = 1109...snip...0847
Nc = 5831...snip...6469

s = Dc * Db * (Nc - Nb) + Dc - Db
p = split_using_lambda(n, abs(s))
q = n / p
assert p * q == n  # yeah!
phi = (p - 1) * (q - 1)
X = inverse(Db, phi) - Nb
Da = inverse(X + Na, phi)
K = pow(V, Da, n)
shared = sha256(long_to_bytes(K)).digest()
aes = AES.new(shared, AES.MODE_GCM, nonce=Nonce)
print aes.decrypt(Body).encode('string-escape')

This prints flag{mission payload}\xb3QM\x1f#\x1e5\xf7=5\x82\xfe|Z\x059.

Conclusion

I was not familiar with the go programming language, but it seems quite easy to pick up, which was a good surprise. Especially, the documentation is clear, which is always a good sign.

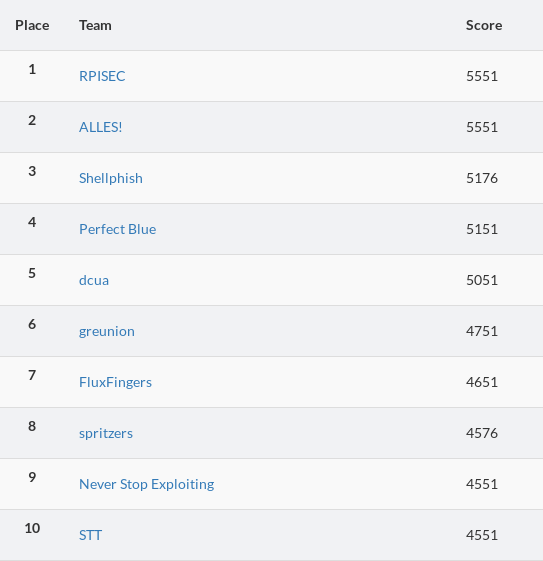
Solving two challenges in a weekend does not seem like much, but we still manage to rank 6 out of the many teams competing, which is nothing to be ashamed of!

Scoreboard